Spss Mixed How to Read Covariance 2,1 1,1
Mixed ANOVA using SPSS Statistics
Introduction
A mixed ANOVA compares the mean differences between groups that have been split on two "factors" (as well known as contained variables), where one gene is a "within-subjects" factor and the other cistron is a "between-subjects" cistron. For example, a mixed ANOVA is oftentimes used in studies where you have measured a dependent variable (e.k., "back pain" or "salary") over two or more time points or when all subjects take undergone two or more atmospheric condition (i.eastward., where "time" or "weather condition" are your "inside-subjects" factor), only also when your subjects take been assigned into two or more separate groups (eastward.k., based on some feature, such as subjects' "gender" or "educational level", or when they have undergone unlike interventions). These groups course your "between-subjects" factor. The chief purpose of a mixed ANOVA is to understand if there is an interaction between these 2 factors on the dependent variable. Earlier discussing this further, accept a look at the examples below, which illustrate the three more common types of study design where a mixed ANOVA is used:
- Study Design #1
- Report Blueprint #2
- Study Pattern #3
Study Design #one
Your within-subjects factor is time.
Your between-subjects cistron consists of conditions (also known as treatments).
Imagine that a health researcher wants to aid suffers of chronic back pain reduce their pain levels. The researcher wants to discover out whether one of two different treatments is more than constructive at reducing hurting levels over time. Therefore, the dependent variable is "back pain", whilst the within-subjects factor is "fourth dimension" and the betwixt-subjects factor is "conditions". More specifically, the two unlike treatments, which are known equally "conditions", are a "massage programme" (handling A) and "acupuncture program" (treatment B). These two treatments reflect the two groups of the "between-subjects" factor.
In total, 60 participants take function in the experiment. Of these 60 participants, 30 are randomly assigned to undergo treatment A (the massage programme) and the other 30 receive handling B (the acupuncture program). Both treatment programmes concluding eight weeks. Over this 8 week flow, back hurting is measured at iii time points, which represents the three groups of the "within-subjects" gene, "time" (i.e., back hurting is measured "at the beginning of the plan" [time bespeak #1], "midway through the programme" [time betoken #2] and "at the end of the program" [time point #iii]).
At the end of the experiment, the researcher uses a mixed ANOVA to determine whether any change in back pain (i.e., the dependent variable) is the result of the interaction betwixt the type of treatment (i.e., the massage programme or acupuncture programme; that is, the "conditions", which is the "between-subjects" factor) and "time" (i.eastward., the within-subjects factor, consisting of 3 time points). If in that location is no interaction, follow-up tests can still be performed to determine whether whatsoever modify in back hurting was simply due to one of the factors (i.e., conditions or time).
Study Blueprint #2
Your inside-subjects factor is time.
Your between-subjects factor is a characteristic of your sample.
Imagine that a researcher wants to determine whether stress levels amongst immature, centre-aged and older people change the longer they are unemployed, besides as understanding whether there is an interaction betwixt age grouping and unemployment length on stress levels. Therefore, the dependent variable is "stress level", whilst the "within-subjects" factor is "time" and the "between-subjects" factor is "age group".
In total, 60 participants have part in the experiment, which are divided into three groups with 20 participants in each group, which reflects the between-subjects factor, "age group" (i.e., the 3 groups are "young", "middle-aged" and "older" unemployed people). The dependent variable, "stress level", is subsequently measured over four fourth dimension points, which reflects the within-subjects factor, "fourth dimension" (i.due east., stress levels are measured "on the first day the participants are unemployed" [time signal #1], "later one calendar month of unemployment" [fourth dimension point #2], "after three months of unemployment" [time point #iii] and "after half dozen months of unemployment" [time point #4]).
At the finish of the experiment, the researcher uses a mixed ANOVA to determine whether any change in stress level (i.e., the dependent variable) is the result of the interaction between age group (i.east., whether participants are "young", "middle-aged" or "older"; the "between-subjects" factor) and "fourth dimension" (i.due east., the length that the groups of people are unemployed; the "within-subjects" factor). If there is no interaction, follow-up tests can yet be performed to make up one's mind whether any change in stress levels was only due to i of the factors (i.east., fourth dimension or age group).
Study Design #iii
Your within-subjects gene consists of weather condition (also known as treatments).
Your between-subjects cistron is a feature of your sample.
Imagine that a psychologist wants to determine the event of exercise intensity on low, taking into account differences in gender. Therefore, the dependent variable is "depression" (measured using a low index that results in a depression score on a continuous scale), whilst the "within-subjects" cistron consists of "conditions" (i.e., 3 types of "practice intensity": "high", "medium" and "low") and the "between-subjects" gene is a "feature" of your sample (i.e., the between-subjects gene, "gender", which consists of "males" and "females"). More than specifically, these iii different "conditions" (also known as "treatments") are a "loftier intensity exercise programme" (treatment A), "medium intensity exercise programme" (treatment B) and "low intensity exercise programme" (treatment C). Each of these three treatments (i.e., treatment A, handling B and treatment C) reflect the three groups of the "within-subjects" factor, "exercise intensity".
In full, 45 participants take part in the experiment. Since "do intensity" is the "within-subjects" factor, this ways that all 45 participants have to undergo all iii treatments: the "high intensity practise programme" (treatment A), "medium intensity exercise program" (treatment B) and "low intensity practice programme" (treatment C). Each treatment lasts 4 weeks. However, the order in which participants receive each treatment differs, with the 45 participants existence randomly split into 3 groups: (a) 15 participants first undergo treatment A (the "high intensity exercise programme"), followed by treatment B (the "medium intensity practice programme"), and finally treatment C (the "low intensity exercise programme"); (b) another 15 participants beginning with handling B, followed past treatment C, and finishing with treatment A; and (c) the final group of 15 participants offset with handling C, followed past treatment A, and finally, treatment B. This is known every bit counterbalancing and helps to reduce the bias that could result from the lodge in which the treatments are provided (although you may not have done this in your research).
At the end of the experiment, the psychologist uses a mixed ANOVA to decide whether any change in depression (i.e., the dependent variable) is the result of the interaction between do intensity (i.e., the "atmospheric condition/treatments", which is the within-subjects gene) and gender (i.e., a "characteristic" of the sample, which acts as the between-subjects factor). If in that location is no interaction, follow-upwards tests can withal be performed to decide whether any change in depression was just due to i of the factors (i.eastward., do intensity or gender).
As mentioned above, the primary purpose of a mixed ANOVA is to empathize if there is an interaction betwixt your inside-subjects gene and between-subjects gene on the dependent variable. Once you have established whether there is a statistically significant interaction, there are a number of unlike approaches to post-obit upwardly the result. In particular, it is important to realize that the mixed ANOVA is an omnibus test statistic and cannot tell you which specific groups inside each factor were significantly different from each other. For example, if i of your factors (eastward.yard., "time") has three groups (e.g., the 3 groups are your 3 time points: "time point 1", "time indicate 2" and "fourth dimension point three"), the mixed ANOVA result cannot tell you whether the values on the dependent variable were different for 1 group (east.g., "Time point 1") compared with some other group (e.g., "Time point 2"). It only tells you that at least two of the iii groups were different. Since you may have three, four, five or more groups in your study design, as well equally two factors, determining which of these groups differ from each other is important. You lot tin can practise this using post hoc tests, which we discuss later in this guide. In improver, where statistically significant interactions are found, yous need to make up one's mind whether there are any "simple main effects", and if there are, what these effects are (once again, we hash out this later in our guide).
If you are unsure whether a mixed ANOVA is appropriate, you lot may likewise want to consider how it differs from a two-style repeated measures ANOVA. Both the mixed ANOVA and ii-manner repeated measures ANOVA involve two factors, also as a desire to understand whether there is an interaction between these 2 factors on the dependent variable. Yet, the cardinal divergence is that a two-way repeated measures ANOVA has ii "inside-subjects" factors, whereas a mixed ANOVA has only ane "within-subjects" factor because the other factor is a "between-subjects" factor. Therefore, in a two-way repeated measures ANOVA, all subjects undergo all conditions (e.g., if the report has two conditions – a control and a treatment – all subjects take office in both the control and the treatment). Therefore, unlike the mixed ANOVA, subjects are not separated into different groups based on some "between-subjects" gene (e.g., a characteristic such equally subjects' "gender" or "educational level", or so that they but receive ane "status": either the control or the treatment). Therefore, if you lot think that the mixed ANOVA is non the exam y'all are looking for, yous may desire to consider a ii-fashion repeated measures ANOVA. Alternately, if neither of these are appropriate, you lot can use our Statistical Test Selector, which is part of our enhanced content, to decide which test is appropriate for your written report pattern.
In this "quick showtime" guide, we show you how to behave out a mixed ANOVA with postal service hoc tests using SPSS Statistics, too as the steps you will demand to go through to interpret the results from this test. Nonetheless, before nosotros innovate you to this process, you need to understand the different assumptions that your data must come across in order for a mixed ANOVA to requite you lot a valid consequence. We discuss these assumptions next.
SPSS Statistics
Assumptions
When y'all choose to analyse your data using a mixed ANOVA, much of the procedure involves checking to make sure that the data you want to analyse can really exist analysed using a mixed ANOVA. Y'all need to do this because it is only appropriate to utilise a mixed ANOVA if your data "passes" 7 assumptions that are required for a mixed ANOVA to give you a valid result. In exercise, checking for these assumptions requires you to use SPSS Statistics to comport out a few more tests, too every bit call up a little bit more about your information. Whilst information technology is not a difficult task, it will take up most of your time when carrying out a mixed ANOVA.
Earlier we introduce you to these seven assumptions, do not be surprised if, when analysing your ain data using SPSS Statistics, one or more of these assumptions is violated (i.e., not met). This is non uncommon when working with real-world data rather than textbook examples. Withal, even when your data fails certain assumptions, there is often a solution to try and overcome this. First, allow'southward take a look at these seven assumptions:
- Assumption #1: Your dependent variable should be measured at the continuous level (i.e., they are either interval or ratio variables). Examples of continuous variables include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so along. Yous can acquire more than well-nigh interval and ratio variables in our article: Types of Variable.
- Supposition #ii: Your within-subjects factor (i.e., within-subjects independent variable) should consist of at to the lowest degree two categorical, "related groups" or "matched pairs". "Related groups" indicates that the same subjects are nowadays in both groups. The reason that it is possible to have the same subjects in each group is because each subject has been measured on two occasions on the aforementioned dependent variable, whether this is at ii different "fourth dimension points" or having undergone two unlike "conditions". For example, you might have measured 10 individuals' performance in a spelling test (the dependent variable) before and later on they underwent a new course of computerized educational activity method to ameliorate spelling (i.e., 2 different "fourth dimension points"). Yous would like to know if the calculator training improved their spelling performance. The offset related grouping consists of the subjects at the first of the experiment, prior to the computerized spelling training, and the second related group consists of the same subjects, just now at the end of the computerized training.
- Assumption #three: Your between-subjects factor (i.e., between-subjects factor independent variable) should each consist of at least two chiselled, "independent groups". Case independent variables that run across this benchmark include gender (2 groups: male or female), ethnicity (iii groups: Caucasian, African American and Hispanic), physical activity level (4 groups: sedentary, low, moderate and high), profession (5 groups: surgeon, physician, nurse, dentist, therapist), and and so forth.
- Assumption #four: At that place should be no significant outliers in any group of your within-subjects factor or betwixt-subjects factor. Outliers are simply single data points inside your data that exercise not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with merely a small variation betwixt students, ane student had a score of 156, which is very unusual, and may fifty-fifty put her in the tiptop ane% of IQ scores globally). The problem with outliers is that they can take a negative event on the mixed ANOVA, distorting the differences between the related groups (whether increasing or decreasing the scores on the dependent variable), which reduces the accuracy of your results. Fortunately, when using SPSS Statistics to run a mixed ANOVA on your data, you can easily detect possible outliers. In our enhanced mixed ANOVA guide, we: (a) show you how to discover outliers using SPSS Statistics, whether you cheque for outliers in your 'actual data' or using 'studentized residuals'; and (b) discuss some of the options you accept in social club to bargain with outliers.
- Supposition #5: Your dependent variable should exist approximately commonly distributed for each combination of the groups of your two factors (i.e., your inside-subjects factor and between-subjects factor). Whilst this sounds a little tricky, it is easily tested for using SPSS Statistics. Also, when we talk about the mixed simply requiring approximately normal information, this is considering information technology is quite "robust" to violations of normality, meaning that assumption can be a niggling violated and notwithstanding provide valid results. You tin can test for normality using, for example, the Shapiro-Wilk test of normality (for 'actual data') or Q-Q Plots (for 'studentized residuals'), both of which are simple procedures in SPSS Statistics. In addition to showing you how to do this in our enhanced mixed ANOVA guide, we also explain what you tin do if your data fails this assumption (i.e., if it fails it more a lilliputian bit).
- Supposition #half-dozen: There needs to be homogeneity of variances for each combination of the groups of your 2 factors (i.e., your inside-subjects factor and between-subjects gene). Again, whilst this sounds a niggling catchy, you tin hands test this assumption in SPSS Statistics using Levene'southward test for homogeneity of variances. In our enhanced mixed ANOVA guide, we (a) show y'all how to perform Levene's examination for homogeneity of variances in SPSS Statistics, (b) explain some of the things you lot will need to consider when interpreting your information, and (c) present possible means to continue with your analysis if your data fails to meet this assumption.
- Assumption #7: Known as sphericity, the variances of the differences between the related groups of the within-subject factor for all groups of the between-subjects factor (i.e., your within-subjects gene and between-subjects factor) must be equal. Fortunately, SPSS Statistics makes information technology easy to test whether your data has met or failed this assumption. Therefore, in our enhanced mixed ANOVA guide, we (a) show yous how to perform Mauchly'due south Exam of Sphericity in SPSS Statistics, (b) explicate some of the things you will need to consider when interpreting your data, and (c) present possible ways to keep with your analysis if your data fails to come across this assumption.
You can cheque assumptions #4, #5, #six and #seven using SPSS Statistics. Just think that if you do not run the statistical tests on these assumptions correctly, the results you go when running a mixed ANOVA might not exist valid. This is why we dedicate a number of sections in our enhanced guide to help you get this right. You lot can discover out virtually our enhanced content as a whole on our Features: Overview page, or more specifically, larn how nosotros assistance with testing assumptions on our Features: Assumptions page.
In the section, Procedure, we illustrate the SPSS Statistics procedure that you can utilize to deport out a mixed ANOVA on your data. First, we introduce the case that is used in this guide.
SPSS Statistics
Instance
A researcher wanted to detect whether the intensity of an exercise-training program, but with equal calorific expenditure, had an effect on cholesterol concentration over a six-month catamenia. Therefore, the dependent variable was "cholesterol concentration", the inside-subjects cistron was "time" and the between-subjects factor was the "weather" (North.B., each of these variables are explained farther below).
To answer this, 60 participants were recruited to take part in the experiment, randomly split into three each groups of 20 participants. Each of these three groups of 20 participants received a dissimilar "status": in one group, participants did not change their current sedentary lifestyle (i.e., this was Group #1, also called the "control" group); in another group, participants underwent a low-intensity do-grooming programme that expended 1000 kCal per week (i.e., this was Group #2, also called "treatment A"); the final group underwent a loftier-intensity exercise-preparation programme that as well expended 1000 kCal per week, but therefore exercised for less full time (i.eastward., this was Group #iii, also called "treatment B"). All of the conditions (i.e., the control, treatment A and treatment B) lasted six months. During this period, the dependent variable, "cholesterol concentration", was measured three times: "at the beginning of the experiment" (fourth dimension point #one), "mid-mode through the six months" (time point #2) and "at the finish of the experiment" (time point #3). These 3 fourth dimension points (i.e., fourth dimension point #1, time signal #2 and time point #3) represent the three groups of the within-subjects factor, "fourth dimension".
SPSS Statistics
Setup in SPSS Statistics
In this example, there are three variables: (one) the dependent variable, cholesterol, which is the cholesterol concentration (in mmol/50); (2) the between-subjects cistron, group, which has three categories: "Command" (command group), "Int_1" (handling A) and "Int_2" (treatment B); and (3) the within-subjects factor, time, which has three categories: "pre", "mid" and "post".
Participants' cholesterol concentration was recorded in the variable pre for pre-intervention, mid for mid-way through and mail service for mail service-intervention. These 3 variables make up the within-subjects factor, time, and the scores within these three variables reflect the dependent variable, cholesterol. The dissimilar interventions were stored in the variable, group, where "Control" is the control group, "Int_1" is the low-intensity training intervention, and "Int_2" is the high-intensity training intervention. In variable terms, the researcher wishes to know if at that place is an interaction between group and fourth dimension on cholesterol.
In our enhanced mixed ANOVA guide, we show you how to correctly enter information in SPSS Statistics to run a mixed ANOVA. Yous can learn about our enhanced data setup content on our Features: Data Setup page. Alternately, come across our generic, "quick outset" guide: Inbound Data in SPSS Statistics.
SPSS Statistics
Test Procedure in SPSS Statistics
The 20 steps below show you how to analyse your data using a mixed ANOVA in SPSS Statistics, including which post hoc examination to select to determine where any differences lie, when none of the seven assumptions in the previous section, Assumptions, have been violated. At the end of these 20 steps, we explain what results you lot will need to interpret from your mixed ANOVA. If yous are looking for help to brand certain your information meets assumptions #4, #5, #half dozen and #7, which are required when using a mixed ANOVA and tin be tested using SPSS Statistics, nosotros testify you how to do this in our enhanced content (run across our Features: Overview page).
Since some of the options in the General Linear Model > Repeated Measures... procedure changed in SPSS Statistics version 25, nosotros show how to carry out a mixed ANOVA in SPSS Statistics versions 25, 26, 27 or 28 (or the subscription version of SPSS Statistics) or version 24 or an earlier version of SPSS Statistics. The latest versions of SPSS Statistics are version 28 and the subscription version. If you are unsure which version of SPSS Statistics you are using, encounter our guide: Identifying your version of SPSS Statistics.
SPSS Statistics versions 25, 26, 27 and 28
(and the subscription version of SPSS Statistics)
- Click Analyze > Meneral Linear Model > Repeated Measures... on the top menu, equally shown below:
Note: In version 27 and the subscription version, SPSS Statistics introduced a new look to their interface called "SPSS Low-cal", replacing the previous look for versions 26 and before versions, which was called "SPSS Standard". Therefore, if you accept SPSS Statistics versions 27 or 28 (or the subscription version of SPSS Statistics), the images that follow will be light grey rather than blue. However, the procedure is identical.
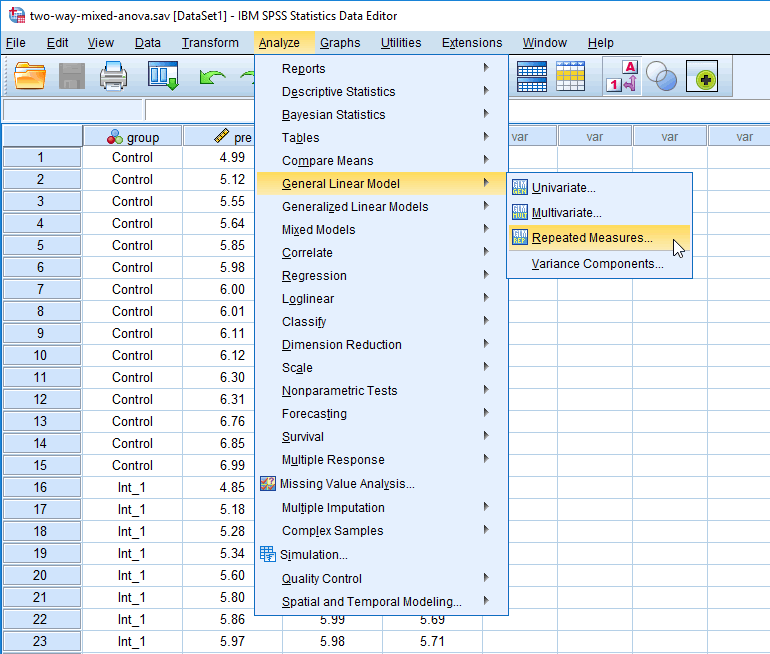
Published with written permission from SPSS Statistics, IBM Corporation.
Yous will be presented with the Repeated Measures Define Factor(s) dialogue box, as shown below:
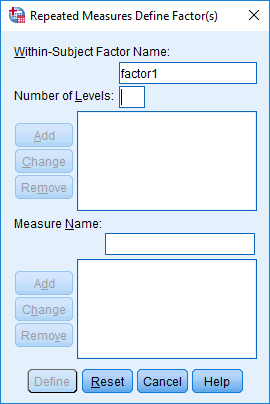
Published with written permission from SPSS Statistics, IBM Corporation.
- In the Westwardithin-Subject Cistron Proper name: box, replace "factor1" with a more meaningful proper name for your within-subjects factor. In this example, replace it with the name "fourth dimension", every bit this reflects the inside-subjects factor, time. Side by side, in the Number of Levels: box, enter the number of time points (i.eastward., the number of levels of the within-subjects factor). In our case, we enter "3", representing pre, mid and post, as shown beneath:
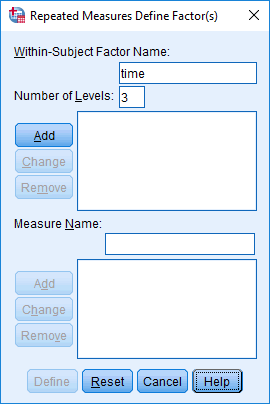
Published with written permission from SPSS Statistics, IBM Corporation.
Click on the![Add]() push and you lot will get the post-obit screen:
push and you lot will get the post-obit screen:

Published with written permission from SPSS Statistics, IBM Corporation.
- In the Measure Due northame: box, enter a name that reflects the name of your dependent variable. Since our dependent variable is cholesterol, nosotros entered "Cholesterol", equally shown below:
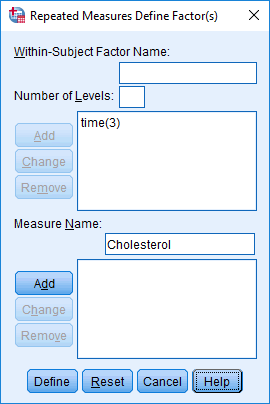
Published with written permission from SPSS Statistics, IBM Corporation.
Click on the![Add]() push button and y'all will become the following screen:
push button and y'all will become the following screen:
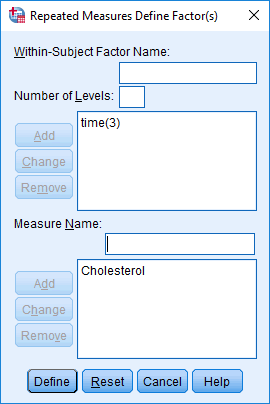
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Define]() push button and you volition be presented with the Repeated Measures dialogue box, equally shown below:
push button and you volition be presented with the Repeated Measures dialogue box, equally shown below: 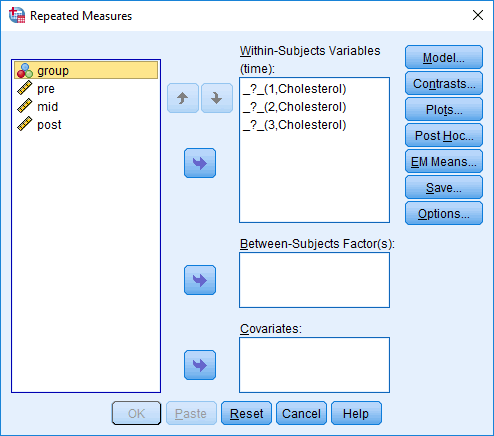
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer pre, mid and post into the Due westithin-Subjects Variables (time): box by highlighting all the variables (clicking on them whilst holding downwards the shift-key) in the left-hand box and clicking on the elevation
![right arrow]() button. You will terminate up with the following screen:
button. You will terminate up with the following screen: 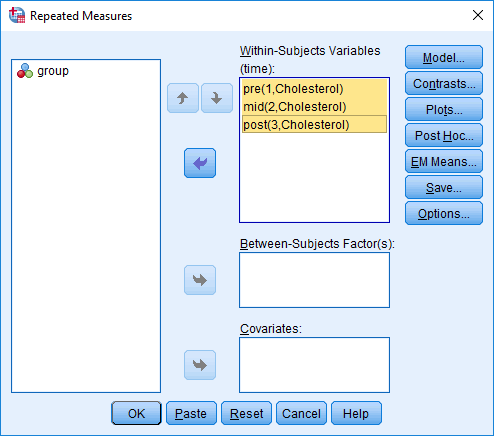
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer the between-subjects factor, group, into the Between-Subjects Cistron(south): box, as shown below:
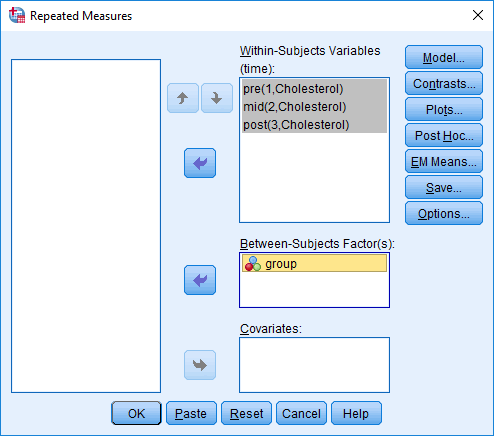
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Plots]() push and you will exist presented with the Repeated Measures: Profile Plots dialogue box, as shown beneath:
push and you will exist presented with the Repeated Measures: Profile Plots dialogue box, as shown beneath: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer group from the Factors: box to the Separate Lines: box and time into the Horizontal Axis: box, as shown below:
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Add]() button and this will add this plot, labelled time*grouping, into the Plotsouth: box, as shown below:
button and this will add this plot, labelled time*grouping, into the Plotsouth: box, as shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() button and you will exist returned to the Repeated Measures dialogue box.
button and you will exist returned to the Repeated Measures dialogue box. - Click on the
![Post Hoc]() button and you will be presented with the Repeated Measures: Post Hoc Multiple Comparisons for Observed Ways dialogue box, as shown beneath:
button and you will be presented with the Repeated Measures: Post Hoc Multiple Comparisons for Observed Ways dialogue box, as shown beneath: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer group from the Factors: box to the Post Hoc Tests For: box by highlighting it and clicking on the
![right arrow]() push. Also, select Tukey from the –Equal Variances Assumed– expanse and Chiliadames-Howell from the –Equal Variances Not Causeless– area. You will stop upwardly with a screen equally shown below:
push. Also, select Tukey from the –Equal Variances Assumed– expanse and Chiliadames-Howell from the –Equal Variances Not Causeless– area. You will stop upwardly with a screen equally shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() button and yous will be returned to the Repeated Measures dialogue box.
button and yous will be returned to the Repeated Measures dialogue box. - Click on the
![Save]() push button and you will be presented with the Repeated Measures: Save dialogue box, as shown below:
push button and you will be presented with the Repeated Measures: Save dialogue box, as shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Select Studentized from the –Residuals– area, every bit shown below:
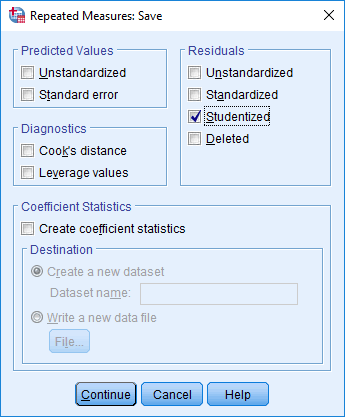
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() push and you will be returned to the Repeated Measures dialogue box.
push and you will be returned to the Repeated Measures dialogue box. - Click on the
![EM Means]() button and yous will be presented with the Repeated Measures: Estimated Margin Ways dialogue box, as shown below:
button and yous will be presented with the Repeated Measures: Estimated Margin Ways dialogue box, as shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer "time", "group" and "group*time" (the interaction term) from the Fthespian(s) and Factor Interactions: box to the Display 1000eans For: box by highlighting them and clicking on the
![right arrow]() button. This will actuate the Compare principal effects checkbox (i.eastward., it will no longer exist greyed out). Tick this checkbox and select
button. This will actuate the Compare principal effects checkbox (i.eastward., it will no longer exist greyed out). Tick this checkbox and select ![Bonferroni]() from the drop-down menu under Conorthwardfidence interval adjustment:. After you accept done all this, you will be presented with the post-obit screen:
from the drop-down menu under Conorthwardfidence interval adjustment:. After you accept done all this, you will be presented with the post-obit screen: 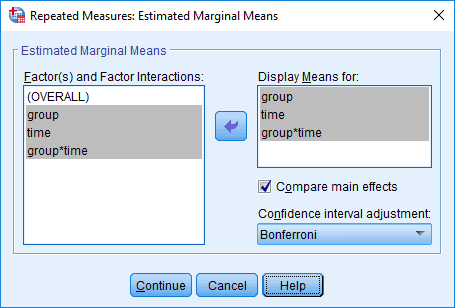
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() button and you volition be returned to the Repeated Measures dialogue box.
button and you volition be returned to the Repeated Measures dialogue box. - Click on the
![Options]() button and you will be presented with the Repeated Measures: Options dialogue box, as shown below:
button and you will be presented with the Repeated Measures: Options dialogue box, as shown below: 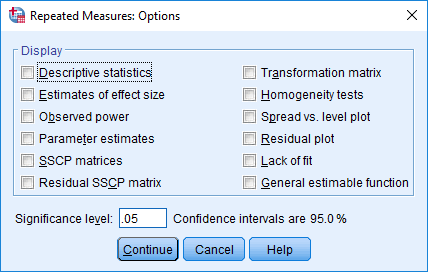
Published with written permission from SPSS Statistics, IBM Corporation.
- In the –Brandish– area, tick the Descriptive statistics, Estimates of effect size and Homogeneity tests checkboxes, equally shown beneath:
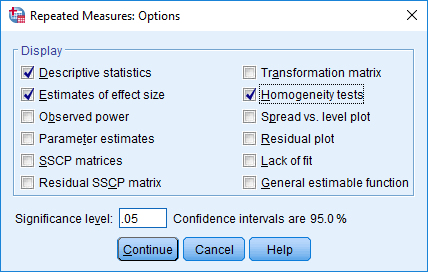
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() push button and you will be returned to the Repeated Measures dialogue box.
push button and you will be returned to the Repeated Measures dialogue box. - Click on the
![OK]() push. This volition generate the output.
push. This volition generate the output.
Now that you have run the General Linear Model > Repeated Measures... process to carry out a two-style mixed ANOVA, go to the Interpreting Results section. You can ignore the section below, which shows you how to carry out a two-way mixed ANOVA if you have SPSS Statistics version 24 or an earlier version of SPSS Statistics.
SPSS Statistics version 24
and earlier versions of SPSS Statistics
- Click Analyze > General Linear Model > Repeated Measures... on the tiptop menu, as shown below:
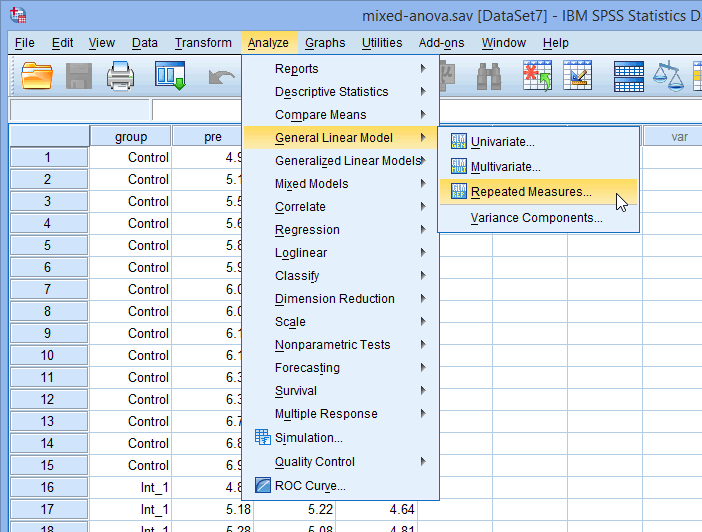
Published with written permission from SPSS Statistics, IBM Corporation.
Yous will be presented with the Repeated Measures Ascertain Cistron(s) dialogue box, every bit shown below:
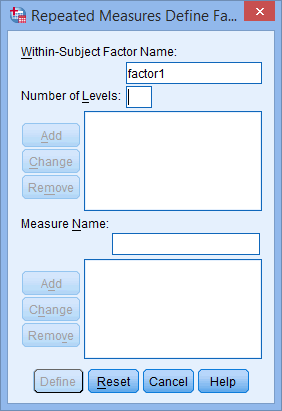
Published with written permission from SPSS Statistics, IBM Corporation.
- In the Due westithin-Subject Factor Name: box, replace "factor1" with a more meaningful name for your within-subject gene. In this example, replace it with the proper name "time", as this reflects the inside-subject gene, fourth dimension. Enter into the Number of Levels: box the number of time points (i.eastward., the number of levels of the within-subject factor). In this case, enter "3", representing pre, mid and post, as shown below:
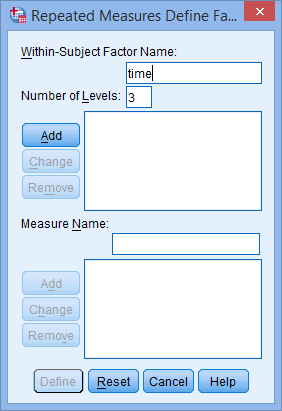
Published with written permission from SPSS Statistics, IBM Corporation.
Click on the![Add]() button and you will get the following screen:
button and you will get the following screen:
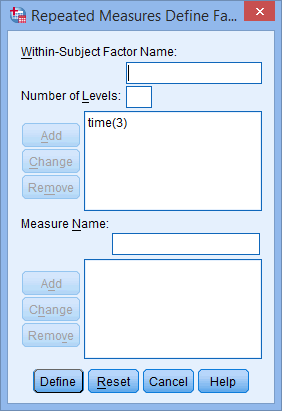
Published with written permission from SPSS Statistics, IBM Corporation.
- Put an appropriate name into the Measure out Name: box. Basically, this is the name of the dependent variable, which is cholesterol in this instance. Therefore, enter "Cholesterol" and click on the
![Add]() push button, and y'all volition end upwardly with the screen beneath:
push button, and y'all volition end upwardly with the screen beneath: 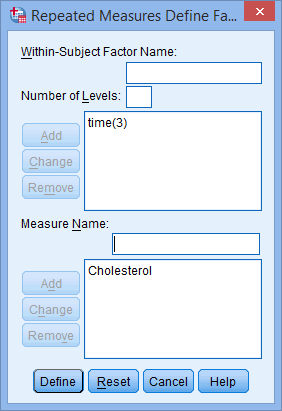
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Define]() push button and you lot will exist presented with the Repeated Measures dialogue box, every bit shown beneath:
push button and you lot will exist presented with the Repeated Measures dialogue box, every bit shown beneath: 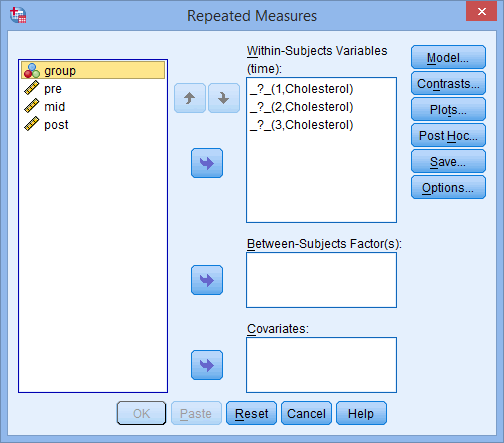
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer pre, mid and post into the Within-Subjects Variables (fourth dimension): box by highlighting all the variables (clicking on them whilst holding down the shift-central) in the left-hand box and clicking the pinnacle
![Right arrow]() button. You will end upwards with the following screen:
button. You will end upwards with the following screen: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer the betwixt-subjects factor, group, into the Between-Subjects Gene(s): box, as shown below:
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Plots]() button and you will be presented with the Repeated Measures: Profile Plots dialogue box, as shown beneath:
button and you will be presented with the Repeated Measures: Profile Plots dialogue box, as shown beneath: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer group from the Factors: box to the Separate Lines: box and fourth dimension into the Horizontal Axis: box, equally shown below:
Published with written permission from SPSS Statistics, IBM Corporation.
Notation: This detail setup works well for this example. Even so, which factor takes the role of the horizontal axis and which the separate lines for your study is upwardly to yous (i.e., whatever makes the most sense to you).
- Click on the
![Add]() push and this will add this plot, labelled "time*group", into the Plots: box, as shown below:
push and this will add this plot, labelled "time*group", into the Plots: box, as shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() button and you will be returned to the Repeated Measures dialogue box.
button and you will be returned to the Repeated Measures dialogue box. - Click on the
![Post Hoc]() button and you will be presented with the Repeated Measures: Postal service Hoc Multiple Comparisons for Observed Means dialogue box, every bit shown below:
button and you will be presented with the Repeated Measures: Postal service Hoc Multiple Comparisons for Observed Means dialogue box, every bit shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer group from the Factors: box to the Post Hoc Tests For: box by highlighting it and clicking on the
![Right arrow]() button. Also, select Tukey from the –Equal Variances Assumed– surface area and Thouames-Howell from the –Equal Variances Not Assumed– expanse. You will cease upwardly with a screen as shown below:
button. Also, select Tukey from the –Equal Variances Assumed– surface area and Thouames-Howell from the –Equal Variances Not Assumed– expanse. You will cease upwardly with a screen as shown below: 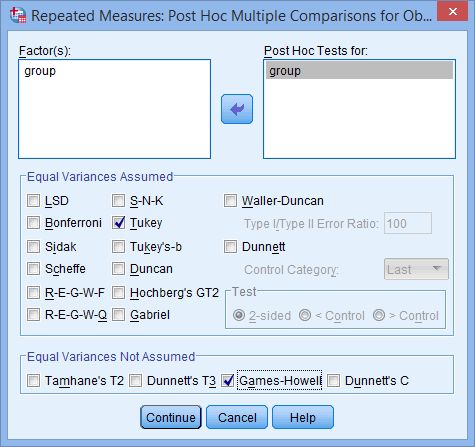
Published with written permission from SPSS Statistics, IBM Corporation.
Note: If your between-subjects factor but has two groups, you lot volition not demand to run any post hoc tests. Call up, these post hoc tests are for the chief effects and not the interaction (i.e., they are not elementary main effects).
- Click on the
![Continue]() button and you lot will be returned to the Repeated Measures dialogue box.
button and you lot will be returned to the Repeated Measures dialogue box. - Click on the
![Save]() button and you will be presented with the Repeated Measures: Save dialogue box, every bit shown below:
button and you will be presented with the Repeated Measures: Save dialogue box, every bit shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Select Southtudentized from the –Residuals– surface area, equally shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() button and you will exist returned to the Repeated Measures dialogue box.
button and you will exist returned to the Repeated Measures dialogue box. - Click on the
![Options]() button and you volition exist presented with the Repeated Measures: Options dialogue box, equally shown beneath:
button and you volition exist presented with the Repeated Measures: Options dialogue box, equally shown beneath: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Transfer time and "grouping*time" (the interaction term) from the Factor(due south) and Gene Interactions: box to the Brandish Means For: box past highlighting them and clicking on the
![Right arrow]() button. This will actuate the Compare main effects checkbox (i.east., it will no longer be greyed out). Tick this checkbox and select "Bonferroni" from the drop-downwardly menu under Confidence interval aligning:. Then, in the –Display– expanse, tick the Descriptive statistics, Eaststimates of effect size and Homogeneity tests checkboxes. After yous take done all this, you lot will be presented with the following screen:
button. This will actuate the Compare main effects checkbox (i.east., it will no longer be greyed out). Tick this checkbox and select "Bonferroni" from the drop-downwardly menu under Confidence interval aligning:. Then, in the –Display– expanse, tick the Descriptive statistics, Eaststimates of effect size and Homogeneity tests checkboxes. After yous take done all this, you lot will be presented with the following screen: 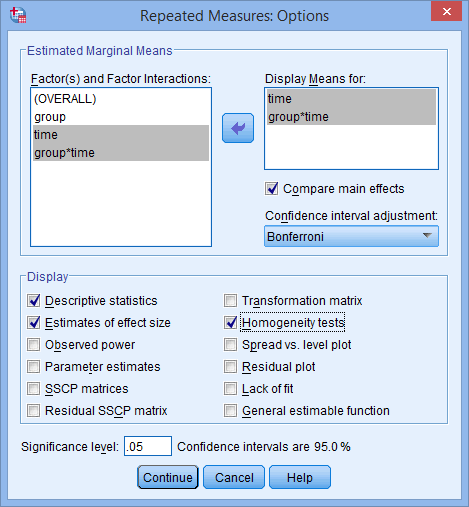
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
![Continue]() button and you volition be returned to the Repeated Measures dialogue box.
button and you volition be returned to the Repeated Measures dialogue box. - Click on the
![OK]() button. This will generate the output.
button. This will generate the output.
SPSS Statistics
Analysing the Output from a Mixed ANOVA
The output generated by SPSS Statistics is quite extensive and can provide a lot of information about your analysis. However, if at that place was a statistically significant interaction between your two factors on the dependent variable, you will need to deport out some additional steps in SPSS Statistics. Below we briefly explain the main steps that yous will demand to follow to interpret your mixed ANOVA results, and where required, perform additional analysis in SPSS Statistics. If yous desire to know how to become through all these sections step-by-stride, together with the relevant SPSS Statistics output, we show you how to practice this in our enhanced mixed ANOVA guide. You can acquire more about our enhanced content in general on our Features: Overview folio. First, take a look through these steps:
- Pace #1: You need to interpret the results from your assumption tests to make sure that you can use a mixed ANOVA to analyse your data. This includes analysing: (a) your actual data or studentized residuals to check that at that place were no significant outliers in any group of your within-subjects gene or between-subjects factor (Assumption #iv); (b) your actual data or studentized residuals to determine that your dependent variable was approximately normally distributed for each combination of the groups of your two factors (Assumption #v); (c) the variances for each combination of groups of your two factors to check for homogeneity of variances (Assumption #6); and (d) the variances of the differences betwixt all combinations of groups of your inside-subjects cistron to check for sphericity (Supposition #vii). This SPSS Statistics output will not just determine whether you have to go back to the commencement of the whole mixed ANOVA process in gild to try and make adjustments to your data so that you lot can utilize this test (east.g., by "transforming" your data), just also what SPSS Statistics output you need to translate later (i.east., based on the results from the Mauchly'southward tests of sphericity, which is used to test supposition #7).
- Pace #2: You need to brand an initial judgement of what your data looks like and whether you might await a statistically pregnant interaction term. You tin do this by interpreting your profile plot. Once you lot have washed this, you can look at the formal statistical test in the Tests of Inside-Subjects Effects SPSS Statistics output to determine whether you do indeed have a statistically significant interaction term. Which part of this output you should translate will depend on whether your data passed the assumptions tests in Step #1 in a higher place.
- Step #3a: If you have a statistically pregnant interaction, reporting the main effects within the Tests of Inside-Subjects Effects SPSS Statistics output can be misleading. Instead, you need to determine the difference between your groups at each level of each factor. Y'all exercise this by analysing your data once more to decide what are known as simple main effects (i.e., rather than main effects). Since you lot accept already gone through the xx steps in SPSS Statistics to a higher place, this is a very quick procedure in SPSS Statistics. Notwithstanding, you need to do this for both factors. For example, using the back hurting instance at the beginning of this guide, you would first be interested in testing the simple main effects of your "between-subjects" factor, the "atmospheric condition" (i.e., this factor as two groups: the "massage programme" and the "acupuncture programme"). This would involves testing for differences in back pain scores (i.e., your dependent variable) between the 2 conditions at each group of the "within-subjects" factor, "time" (i.e., you are testing for differences between the ii conditions at each of the three fourth dimension points: "at the beginning of the programme", "midway through the plan" and "at the end of the programme"). You and then demand to this all over once again, but this time, focusing on the elementary main effects of your within-subjects cistron, "time". Afterwards carrying out these simple main effects procedures in SPSS Statistics, you demand to interpret the profile plots that are produced, besides as the new SPSS Statistics output in the Mauchly'southward Examination of Sphericity, Tests of Within-Subjects Furnishings and Pairwise Comparisons tables. You are now in a position to write up all of your results.
- Step #3b: If y'all exercise not take a statistically pregnant interaction, you demand to interpret and written report the primary effects within the Tests of Inside-Subjects Effects SPSS Statistics output tables (i.east., rather than calculating simple main effects, which you do when the interaction is statistically significant). You have to interpret the main effects for both factors (i.east., the "inside-subjects" factor and "between-subjects" cistron). In addition, if either of these chief effects is statistically significant, you will need to interpret the relevant SPSS Statistics output from your post hoc tests in the Pairwise Comparisons tabular array. This volition help you lot to understand where the differences between the groups inside your factors lie (due east.g., from our back pain example, the differences in back pain betwixt the two "weather condition": the "massage plan" and the "acupuncture programme").
For a statistically significant interaction
If you lot do not accept a statistically pregnant interaction
If y'all are unsure how to translate your mixed ANOVA results or how to check for the assumptions of the mixed ANOVA, bear out transformations using SPSS Statistics, or bear additional SPSS Statistics procedures to run simple main furnishings on your data (meet Pace #3a), we show you how to do this in our enhanced mixed ANOVA guide. We also show you how to write up the results from your assumptions tests and mixed ANOVA output if you need to study this in a dissertation/thesis, assignment or research study. We practise this using the Harvard and APA styles. You can learn more near our enhanced content on our Features: Overview folio.
Source: https://statistics.laerd.com/spss-tutorials/mixed-anova-using-spss-statistics.php





































0 Response to "Spss Mixed How to Read Covariance 2,1 1,1"
Post a Comment